Gridding with Splines in Tension

Next: Preprocessing Up: Gridding of arbitrarily spaced Previous: Exercises

Gridding with Splines in Tension

As an alternative, we may use a global procedure to grid our data. This approach, implemented in the program surface , represents an improvement over standard minimum curvature algorithms by allowing users to introduce some tension into the surface. Physically, we are trying to force a thin elastic plate to go through all our data points; the values of this surface at the grid points become the gridded data. Mathematically, we want to find the function z(x, y) that satisfies the following constraints:

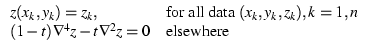
$\begin{array}{ll} z(x_k, y_k) = z_k, & \mbox{for all data $(x_k, y_k, z_k), k =1,n$ } \\ (1-t)\nabla^4 z - t \nabla^2 z = 0 & \mbox{elsewhere} \end{array}$

where t is the ``tension'', $0 \leq t \leq 1$ . Basically, as $t \rightarrow 0$ we obtain the minimum curvature solution, while as $t \rightarrow \infty$ we go towards a harmonic solution (which is linear in cross-section). The theory behind all this is quite involved and we do not have the time to explain it all here, please see Smith and Wessel [1990] for details. Some of the most important switches for this program are indicated in Table 3.3 ^3.1.

Table 3.3: Some of the options in surface

Option	Purpose
-–A aspect	Sets aspect ratio for anisotropic grids.
-–C limit	Sets convergence limit. Default is 1/1000 of data range.
-–T tension	Sets the tension [Default is 0]

Next: Preprocessing Up: Gridding of arbitrarily spaced Previous: Exercises

Paul Wessel
1999-06-09