Nearest neighbor gridding

  

Figure 3.1: Search geometry for nearneighbor 

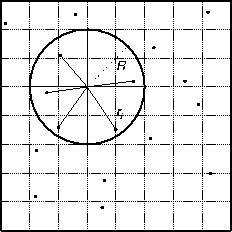
The GMT program nearneighbor  implements a simple ``nearest neighbor'' averaging operation. It is the preferred way to grid data when the data density is high. nearneighbor  is a local procedure which means it will only consider the control data that is close to the desired output grid node. Only data points inside a search radius will be used, and we may also impose the condition that each of the n sectors must have at least one data point in order to assign the nodal value. The nodal value is computed as a weighted average of the nearest data point per sector inside the search radius, with each point weighted according to its distance from the node as follows:

$$\bar{z} = \frac{\sum_{i=1}^{n} z_{i} w_{i}}{\sum_{i=1}^{n} w_... ...d w_{i} = \left( 1 + \frac{9 r_{i}^{2}}{R^{2}} \right) ^{-1}$$

 

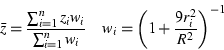
The most important switches are listed in Table 3.2.

 

Table 3.2: Switches used with the nearneighbor  program

Option	Purpose
-–S radius[ k]	Sets search radius. Append k to indicate radius in kilometers [Default is x-units]
-E empty	Assign this value to unconstrained nodes [Default is NaN]
-–N sectors	Sector search, indicate number of sectors [Default is 4]
-–W	Read relative weights from the 4th column of input data

 

We will grid the data in the file ship.xyz which contains ship observations of bathymetry off Baja California. We desire to make a 5' by 5' grid. Running minmax  on the file yields

ship.xyz: N = 82970	<245/254.705>	<20/29.99131>	<-7708/-9>

so we choose the region accordingly:

nearneighbor –-R245/255/20/30 –-I5m -–S40k –-Gship.grd –-V ship.xyz

We may get a view of the contour map using

 
grdcontour ship.grd –-JM6i –-P –-B2 -–C250 –-A1000 | ghostview -